A fast score-based search algorithm for maximal ancestral graphs using entropy
Paper and Code
Feb 07, 2024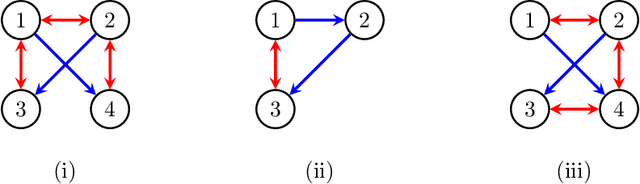

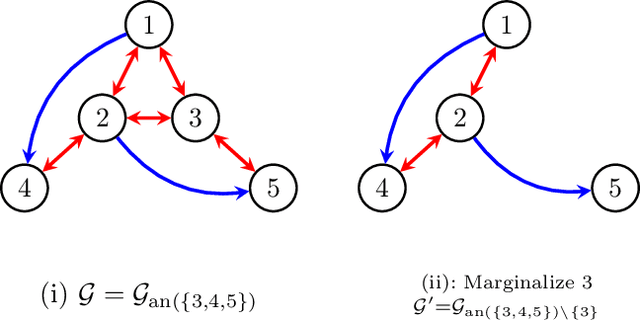
\emph{Maximal ancestral graph} (MAGs) is a class of graphical model that extend the famous \emph{directed acyclic graph} in the presence of latent confounders. Most score-based approaches to learn the unknown MAG from empirical data rely on BIC score which suffers from instability and heavy computations. We propose to use the framework of imsets \citep{studeny2006probabilistic} to score MAGs using empirical entropy estimation and the newly proposed \emph{refined Markov property} \citep{hu2023towards}. Our graphical search procedure is similar to \citet{claassen2022greedy} but improved from our theoretical results. We show that our search algorithm is polynomial in number of nodes by restricting degree, maximal head size and number of discriminating paths. In simulated experiment, our algorithm shows superior performance compared to other state of art MAG learning algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge