A Dynamic Programming Algorithm for Inference in Recursive Probabilistic Programs
Paper and Code
Sep 10, 2012
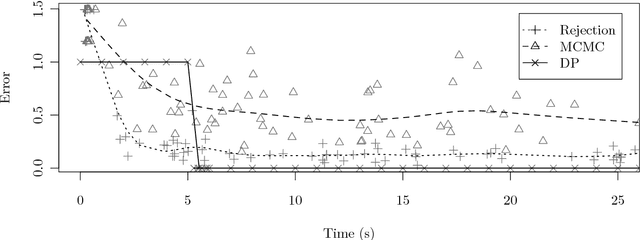

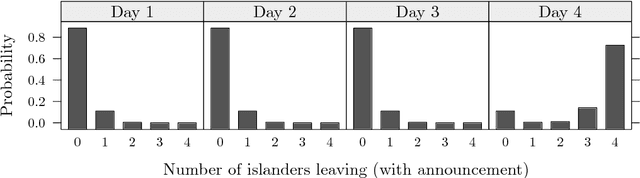
We describe a dynamic programming algorithm for computing the marginal distribution of discrete probabilistic programs. This algorithm takes a functional interpreter for an arbitrary probabilistic programming language and turns it into an efficient marginalizer. Because direct caching of sub-distributions is impossible in the presence of recursion, we build a graph of dependencies between sub-distributions. This factored sum-product network makes (potentially cyclic) dependencies between subproblems explicit, and corresponds to a system of equations for the marginal distribution. We solve these equations by fixed-point iteration in topological order. We illustrate this algorithm on examples used in teaching probabilistic models, computational cognitive science research, and game theory.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge