A Connection between Feed-Forward Neural Networks and Probabilistic Graphical Models
Paper and Code
Oct 30, 2017
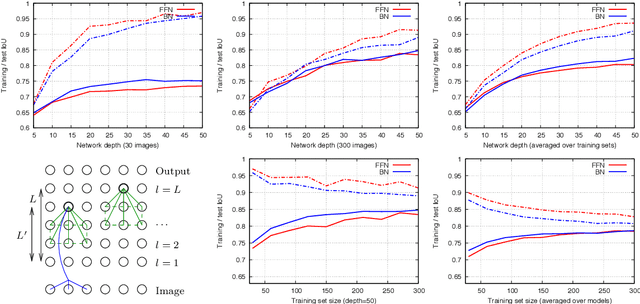

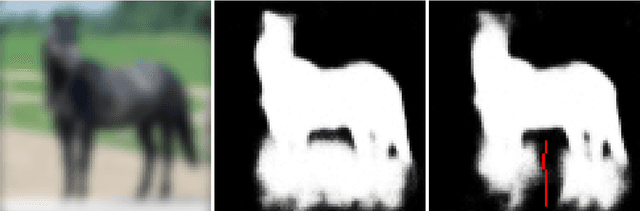
Two of the most popular modelling paradigms in computer vision are feed-forward neural networks (FFNs) and probabilistic graphical models (GMs). Various connections between the two have been studied in recent works, such as e.g. expressing mean-field based inference in a GM as an FFN. This paper establishes a new connection between FFNs and GMs. Our key observation is that any FFN implements a certain approximation of a corresponding Bayesian network (BN). We characterize various benefits of having this connection. In particular, it results in a new learning algorithm for BNs. We validate the proposed methods for a classification problem on CIFAR-10 dataset and for binary image segmentation on Weizmann Horse dataset. We show that statistically learned BNs improve performance, having at the same time essentially better generalization capability, than their FFN counterparts.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge