A Competitive Learning Approach for Specialized Models: A Solution for Complex Physical Systems with Distinct Functional Regimes
Paper and Code
Jul 21, 2023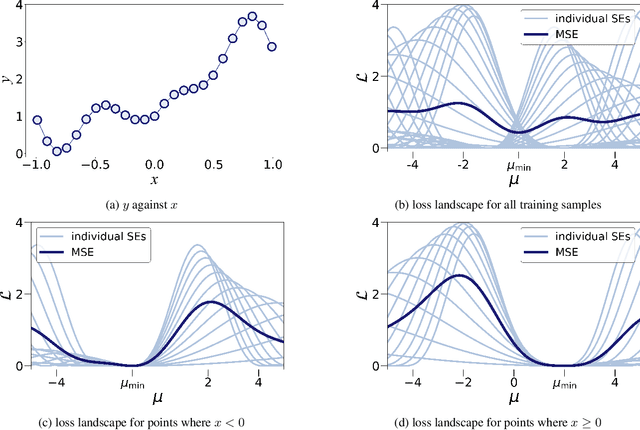
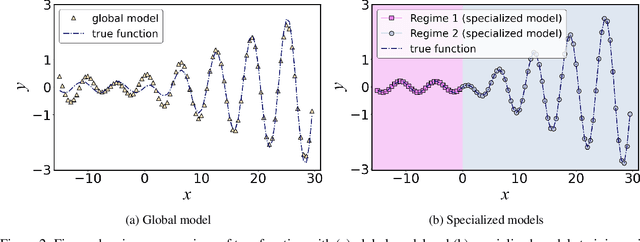
Complex systems in science and engineering sometimes exhibit behavior that changes across different regimes. Traditional global models struggle to capture the full range of this complex behavior, limiting their ability to accurately represent the system. In response to this challenge, we propose a novel competitive learning approach for obtaining data-driven models of physical systems. The primary idea behind the proposed approach is to employ dynamic loss functions for a set of models that are trained concurrently on the data. Each model competes for each observation during training, allowing for the identification of distinct functional regimes within the dataset. To demonstrate the effectiveness of the learning approach, we coupled it with various regression methods that employ gradient-based optimizers for training. The proposed approach was tested on various problems involving model discovery and function approximation, demonstrating its ability to successfully identify functional regimes, discover true governing equations, and reduce test errors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge