A Bandit Approach with Evolutionary Operators for Model Selection

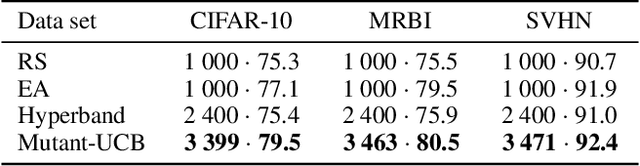
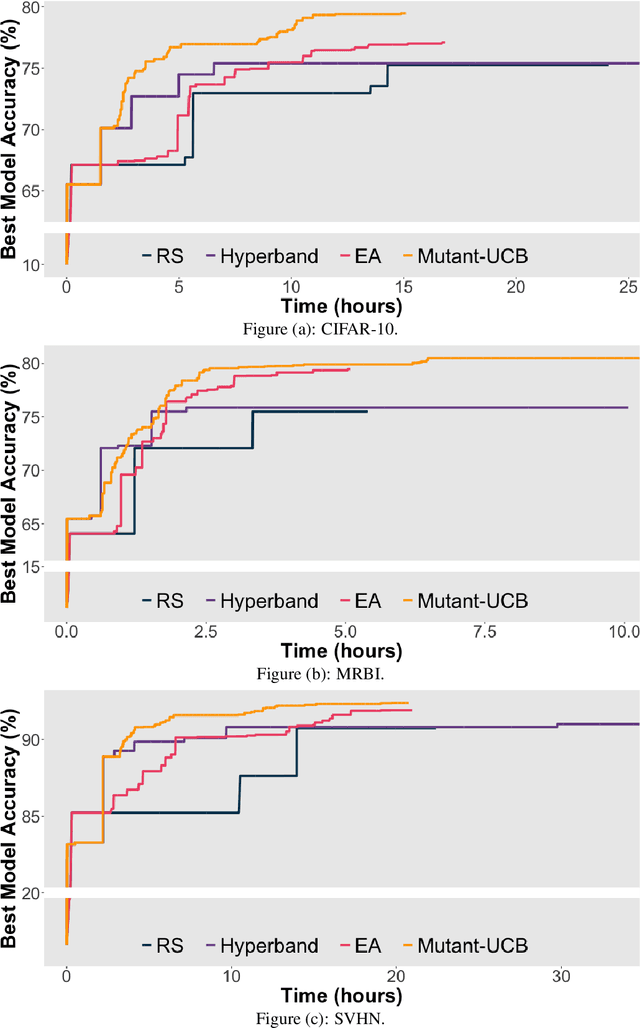
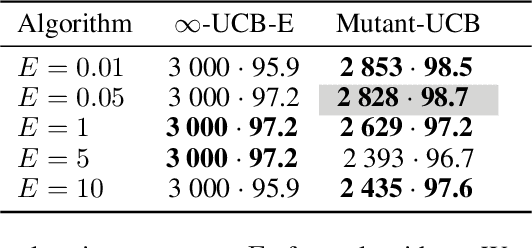
This paper formulates model selection as an infinite-armed bandit problem. The models are arms, and picking an arm corresponds to a partial training of the model (resource allocation). The reward is the accuracy of the selected model after its partial training. In this best arm identification problem, regret is the gap between the expected accuracy of the optimal model and that of the model finally chosen. We first consider a straightforward generalization of UCB-E to the stochastic infinite-armed bandit problem and show that, under basic assumptions, the expected regret order is $T^{-\alpha}$ for some $\alpha \in (0,1/5)$ and $T$ the number of resources to allocate. From this vanilla algorithm, we introduce the algorithm Mutant-UCB that incorporates operators from evolutionary algorithms. Tests carried out on three open source image classification data sets attest to the relevance of this novel combining approach, which outperforms the state-of-the-art for a fixed budget.